|
The Old-Fashioned Method
of Finding Square Roots |
This method is much like long division except that each step the divisor is changed.
Remember the steps for long division.
1.-
Divide
2.-
Multiply
3.-
Subtract
|
3 --------Quotient Divisor ----- 13/44 ----- Dividend
- 39 5 ------ Remainder
|
Example 1
|
Find
the square root of 4225 or √
4225 |
Step A
Separate the number 4225 into two-digit “groups” beginning at decimal point.
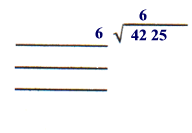 |
Step B
For the first trial divisor, take the square root of the largest perfect square root of the largest perfect square which is less than the first group ( √ 42 ).
In this case is 6 because 62 or 36 is the largest perfect square less than 42.
Write the 6 on top of 42 then multiply 6*6 and subtract the answer from 42.
6
is the first digit of the square root of
4225
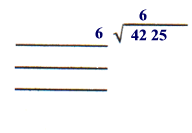 |
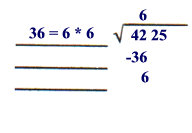 |
Step C
Bring down the next two digits.
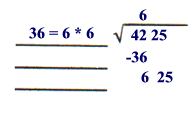 |
Step D
In this step we find the next quotient or the last digit of the square root of 4225.
First take the quotient (6) and add it to the old divisor (6) to get the "partial" new divisor.
It is called "partial" divisor because we still have to find the last digit to complete this divisor. This last digit is also the last digit of the square root of 4225. The parenthesis ( ) indicates the location of this digit.
Old quotient + old divisor = 6 + 6 = 12 .
12 is the "partial" new divisor.
Set down the 12 so as to leave a space for ( ).
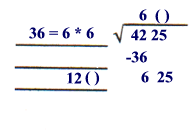 |
Step E
The last digit ( ) has to be 9 or less.
If
you multiply 12(
) * (
) the answer should be equal or less than the remainder
625.
There are many tricks to find ( ).
Estimate using the following values: 120 for 12( ) and 600 for 625
Now think! How many 120's go into 600 ? five (5)
Then multiply 125 * 5 = 625 , this is good because the product is less or equal than 625.
 |
|
The
answer of the square root of 4225
is 65
because 65 * 65 =
4225 |
Note
Lets assume that the product of 125 * 5 is a number more than the remainder 625, then you have to try the numbers 4, 3, 2,or 1 respectively until the product of 12( ) * ( ) is less or equal than 625.
In other words
124*4
123*3
122*2
121*1
EXAMPLE 2
| Find the square root of 4741 to three-figure accuracy |
Step A
Separate the numbers into groups of two.
Add four zeros to get two decimals.
 |
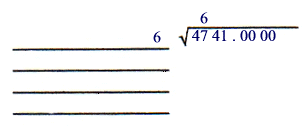
Step B
For the first divisor take the square root of the largest perfect square root which is
less than 47.
| 6*6 = 36 is the closest choice to 47 |
 |
Step C
Multiply, subtract and bring down the next two digits.
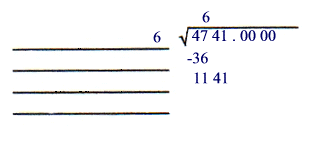 |
Step D
To get the next "partial" trial divisor follow the next two steps.
---- Add the previous quotient (6) to the last divisor (6) to get 12( ).
----The ( ) in 12( ) indicates the missing digit to be found.
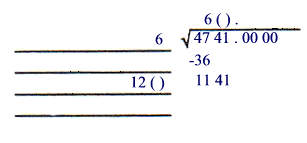 |
Step E
To find the missing digit approximate how many 120's go into1141.
A better way, approximate how many 12's go into 114.
|
114/12 approximate 9.5
------
use 9 to check
12 ( 9 ) * ( 9 ) = 1161 Since 1161 is more than 1141 ( the last remainder ) try 8 12( 8 ) * ( 8 ) = 1024 1024 is less than 1141 8 is the next missing digit that takes place instead of the parenthesis
|
Step F
-----Multiply and subtract as in long division.
-----Then bring down the next two zeros.
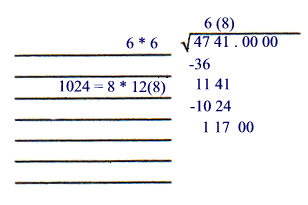 |
Step G
To find the next "partial" trial divisor add the previous divisor ( 128 ) to the previous
quotient ( 8 ) to get 136.
| 136( ) is the next "partial" trial divisor |
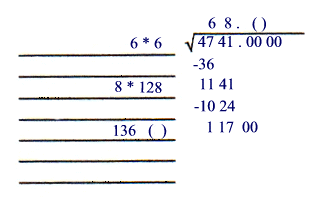 |
Step H
To find the missing digit in parenthesis, approximate how many 1360's go onto 11700.
A better way, approximate how many 13's go into 117.
| The answer is 9
Check 136 ( 9 ) * 9 = 12321 The number 12321 is more than the last divisor 11700 ( this number is not good ) Try 8 136 ( 8) * 8 = 10944 The number 10944 is less than the last remainder 11700 ( good! )
|
Step I
-----Multiply and subtract as in long division.
------Then bring down the next two zeros.
 |
Step J
To find the next "partial" trial divisor add the last quotient (1368) to the last divisor (8).
| 1368 + 8 = 1376
1376 ( ) is the next "partial" divisor The parenthesis indicates the missing digit to be found by trial. |
 |
Step K
To find the missing digit inside the parenthesis approximate how many 13760's
go into 75600.
A better way, approximate how many 13's go into 75.
| The answer is 5
Check 1376 ( 5 ) * 5 = 68825 The number 68825 is less than the last remainder 75600 ( good! ) |
Step L
-----Multiply and subtract as in long division.
-----There are no more digits to bring down.
 |
| The answer 68.85 to three-digit accuracy is 68.9 |